┬δα±≥ΦΓε±≥│ ≡Φ±≤Γαδⁿφε┐ ∩δε∙ΦφΦ
┬δα±≥ΦΓε±≥│
≡Φ±≤Γαδⁿφε┐ ∩δε∙ΦφΦ ∞εµφα τ∞│φ■Γα≥Φ
Σαφ≤ ≡Φ±≤Γαδⁿφ≤ ∩δε∙Φφ≤, ΓΦπδ Σ ≤ΓσΣσφε┐ ±Φ±≥σ∞Φ Ωεε≡ΣΦφα≥, α ≥αΩεµ
±│≥ΩΦ. ╩≡│∞ ≥επε ∞εµφα ΓΦτφα≈α≥Φ ≤∞εΓΦ, Ω│ Γ∩δΦΓα■≥ⁿ φα ∩εΓεΣµσφφ
εß'║Ω≥α ≡Φ±≤Γαδⁿφε┐ ∩δε∙ΦφΦ. ╥αΩ│ τ∞│φΦ ∩≡εΓεΣ ≥ⁿ± ≈σ≡στ
αΩ≥ΦΓα÷│■ Ωε∞αφΣΦ "╟αΩ≡Φ≥Φ" αßε "╟α±≥ε±≤Γα≥Φ".
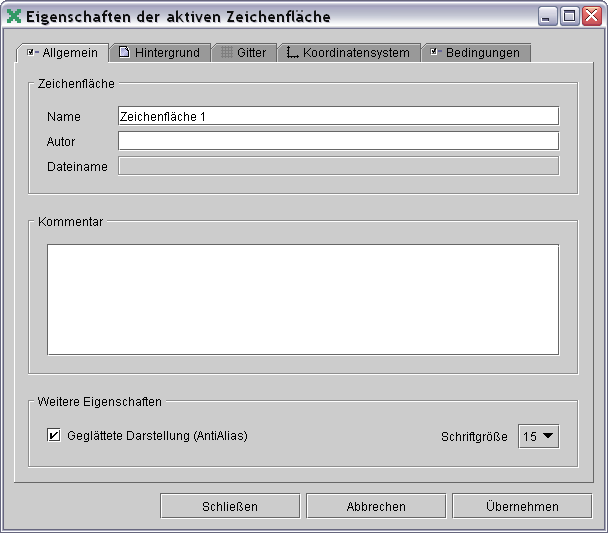
╩εµφα Ωεφ±≥≡≤Ω÷│
∞α║ ±Γε║ │∞' φα
≥Φ≥≤δⁿφ│Θ ±≥ε≡│φ÷│ (φα∩≡ΦΩδαΣ, ≡Φ±≤Γαδⁿφα ∩δε∙Φφα 5), Ωσ ∞εµφα
τ∞│φΦ≥Φ Γ ∩εδ│ "▓∞' ".╙ Γ│Σ∩εΓ│ΣφΦ⌡ ∩εδ ⌡ ∞εµφα ΣεΣα≥Φ ≥αΩεµ │∞' αΓ≥ε≡α │ Ωε∞σφ≥α≡.
" ▓∞' ⌠αΘδα" ∩εΩατ≤║, Γ Ωε∞≤ ⌠αΘδ│ τßσ≡│πα║≥ⁿ±
αΩ≥ΦΓφα ≡Φ±≤Γαδⁿφα
∩δε∙Φφα.
Unter "Weitere Eigenschaften" kann die "GeglΣttete
Darstellung (AntiAlias)" durch das KontrollkΣstchen ein- und
ausgeschalten werden.
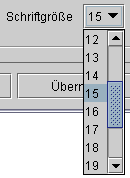
Die Schriftgr÷▀e der Objektnamen und der Texte der ZeichenflΣche lΣsst
sich ⁿber die Auswahlliste "Schriftgr÷▀e" beeinflussen. Die
Standardgr÷▀e betrΣgt 15.
╨ετ∞│≡ °≡Φ⌠≥α φατΓ εß'║Ω≥│Γ ≥α ≥σΩ±≥≤ φα ≡Φ±≤Γαδⁿφ│Θ ∩δε∙Φφ│ Γ±≥αφεΓδ■║≥ⁿ± Γ "╨ετ∞│≡ °≡Φ⌠≥α". ╤≥αφΣα≡≥φΦΘ ≡ετ∞│≡ 15.
─ε ∩ε≈α≥Ω≤
±≥ε≡│φΩΦ
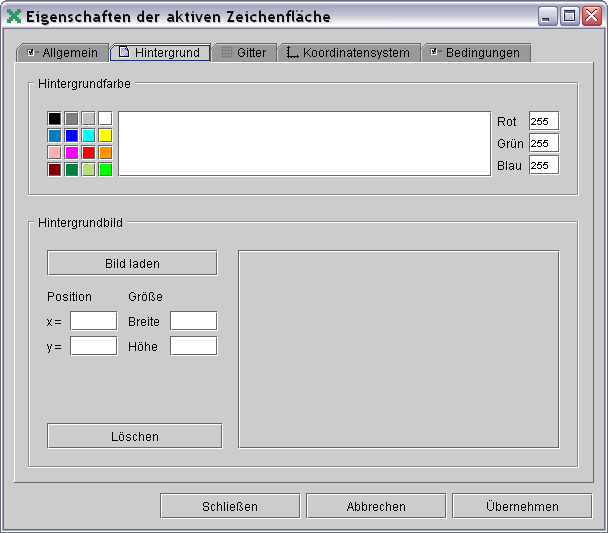
─ε≥≡Φ∞≤■≈Φ±ⁿ ±≥αφΣα≡≥≤, ≡Φ±≤Γαδⁿφα ∩δε∙Φφα ≤ GEONExT ∞α║
ß│δΦΘ Ωεδ│≡.
╩εδ│≡ Σ≡≤πεπε ∩δαφ≤ ∞εµφα ΓΦß≡α≥Φ Γ ∩αδ│≥≡│ Ωεδⁿε≡│Γ.
┘εß ∩≡ΦΓ' τα≥Φ Ωα≡≥ΦφΩ≤ Σ≡≤πεπε ∩δαφ≤ Σε ≡Φ±≤Γαδⁿφε┐ ∩δε∙ΦφΦ,
Σε±≥α≥φⁿε εΣΦφ ≡ατ φα≥Φ±φ≤≥Φ ∞Φ°Ωε■ φα "╟απ≡≤τΦ≥Φ Ωα≡≥ΦφΩ≤".
┬│ΣΩ≡Φ║≥ⁿ± Γ│Ωφε Σε∩ε∞επΦ, Γ Ωε∞≤ ΓΦßΦ≡α║≥ⁿ± ⌠αΘδ τεß≡αµσφφ
(⌠ε≡∞α≥ GIF, JPG αßε PNG).
╧ετΦ÷│■ │ ≡ετ∞│≡ Ωα≡≥ΦφΩΦ ∞εµφα τ∞│φΦ≥Φ, Ω∙ε ≤ Γ│Σ∩εΓ│Σφε∞≤ ∩εδ│
φΦµφⁿεπε δ│Γεπε Ω≤≥α ταΣα≥Φ Γ εΣΦφΦ÷ ⌡ ∞α±°≥αß≤ Ωεε≡ΣΦφα≥Φ X ≥α Y, α
≥αΩεµ °Φ≡Φφ≤ ≥α ΓΦ±ε≥≤
τεß≡αµσφφ .
╩ε∞αφΣε■ "┬ΦΣαδΦ≥Φ" Ωα≡≥ΦφΩα Σ≡≤πεπε ∩δαφ≤ ∩≡ΦßΦ≡α║≥ⁿ± .
╧≡Φ∞│≥Ωα
╧≡Φ τßσ≡σµσφφ│ ≡Φ±≤Γαδⁿφε┐ ∩δε∙ΦφΦ τεß≡αµσφφ Σ≡≤πεπε ∩δαφ≤
τα∩Φ±≤║≥ⁿ± ≤ ⌠αΘδ GEONExT.
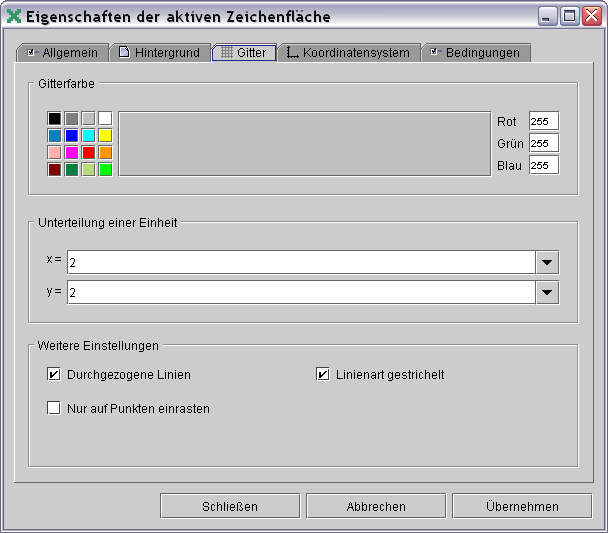
─δ ÷ⁿεπε ∞εµφα Ωε≡Φ±≥≤Γα≥Φ±ⁿ τα∩≡ε∩εφεΓαφΦ∞Φ ΓσδΦ≈Φφα∞Φ αßε ταΣαΓα≥Φ ┐⌡ ±α∞ε±≥│Θφε.
▀Ω∙ε Γ│Σ±≥αφⁿ ∞│µ ΣΓε∞α δ│φ│ ∞Φ ≡σ°│≥ΩΦ ║ ∞σφ°ε■, φ│µ Σσ± ≥ⁿ ∩│Ω±σδ│Γ σΩ≡αφ≤, ≥ε ÷│ δ│φ│┐ φσ Σσ∞εφ±≥≡≤■≥ⁿ± .
▀Ω∙ε ∩≡α÷■║ Ωε∞αφΣα
╧≡ΦΓ' τα≥Φ, ≥ε ≥ε≈ΩΦ ταΩ≡│∩δ■■≥ⁿ± ≤
≡α±≥≡ ≡Φ±≤Γαδⁿφε┐ ∩δε∙ΦφΦ. ▀Ω∙ε ΓΦß≡α≥Φ "╧≡ΦΓ' τα≥Φ ≥│δⁿΩΦ
τα ≥ε≈ΩΦ", ≥ε ≡≤⌡δΦΓ│
≥ε≈ΩΦ ταΩ≡│∩δ■■≥ⁿ± φα Γµσ │±φ≤■≈Φ⌡.
"╧│Ω±σδ│ τα εΣΦφΦ÷■" φατΦΓα■≥ⁿ ≈Φ±δε ∩│Ω±σδ│Γ σΩ≡αφ≤, Ωσ
Γ│Σ∩εΓ│Σα║ ΣεΓµΦφ│ εΣΦφΦ÷│ ∩≡Φ τß│δⁿ°σφφ│ φα σΩ≡αφ│ 
┬ "╧│Σ∩Φ± Γ│±│" τα∩Φ±≤■≥ⁿ± Γ│±│.
▀Ω∙ε ∩ετφα≈Φ≥Φ Γ│Ωεφ÷σ "╧εΩατα≥Φ εΣΦφΦ÷■", ≥ε Γ δ│Γε∞≤ Γσ≡⌡φⁿε∞≤ Ω≤≥≤ ≡Φ±≤Γαδⁿφε┐ ∩δε∙ΦφΦ τ' Γδ ║≥ⁿ± Γ│Σ≡│τεΩ ΣεΓµΦφε■ 1 εΣΦφΦ÷ .
"╤⌡εΓα≥Φ ∩│Σ∩Φ±" ∩εΩατ≤║ ΓΦß≡αφ≤ Γ│±ⁿ ßστ
÷Φ⌠≡εΓεπε ∩│Σ∩Φ±≤.
└Ω≥ΦΓ≤■≈Φ "╩≡α≥φσ",
≈Φ±δα φα Γ│± ⌡ εΣσ≡µ≤■≥ⁿ εΣΦφΦ÷│. ═α∩≡ΦΩδαΣ, τα∩Φ± "╩≡α≥φσ Γ│Σ" cm, ∩≡ΦτΓεΣΦ≥ⁿ Σε τα∩Φ±≤ φα Γ│± ⌡ 1
cm, 2 cm, 3
cm ...
▀Ω∙ε ±≥αφΣα≡≥φΦ∞ ≈Φφε∞ αΩ≥ΦΓεΓαφΦΘ τα∩Φ± "┬│±ⁿ Ω εß'║Ω≥",
≥ε ≥α
≈Φ │φ°α Γ│±ⁿ ∩≡Φ ΓΩδ■≈σφ│Θ ±Φ±≥σ∞│ Ωεε≡ΣΦφα≥ ∩≡σΣ±≥αΓδσφα φα
≡Φ±≤Γαδⁿφ│Θ ∩δε∙Φφ│ Ω ∩≡ ∞α. ╧≡Φ ÷ⁿε∞≤ ≥ε≈ΩΦ ∩σ≡σ≥Φφ≤ ∞εµφα εΣσ≡µα≥Φ
τα
Σε∩ε∞επε■ Γ│±σΘ, α ≥ε≈ΩΦ, Ω│ ≡ετ≥α°εΓαφ│ φα Γ│± ⌡, Σσ∞εφ±≥≡≤■≥ⁿ± Ω
ΩεΓτφ│ ≥ε≈ΩΦ.
"╙∞εΓΦ" ≡Φ±≤Γαδⁿφε┐ ∩δε∙ΦφΦ ∞α■≥ⁿ Γ∩δΦΓ φα ΓΦπδ Σ │ ∩εΓεΣµσφφ
εß'║Ω≥α. ╧│±δ Ωεµφε┐ φεΓε┐ ε∩σ≡α÷│┐ τ εß'║Ω≥ε∞ ≡Φ±≤Γαδⁿφε┐
∩δε∙ΦφΦ αφαδ│τ≤■≥ⁿ± ≤∞εΓΦ.
"╙∞εΓα" ∞α║ ≥αΩ≤ ±≥≡≤Ω≥≤≡≤:
- │'∞ .Ωδ■≈εΓσ ±δεΓε=∩│Σ≡α⌡≤φεΩ
Algebra Systems . ╧εΣαδⁿ°≤
│⌠ε≡∞α÷│■ ±δ│Σ °≤Ωα≥Φ Γ ≡ετΣ│δ│
|
─εΣα≥εΩ Σε ≤∞εΓ
╤∩ε≈α≥Ω≤ ΓΦτφα≈α║≥ⁿ± ≤∞εΓα. ─δ ÷ⁿεπε ∩ε≥≡│ßφε φα≥Φ±φ≤≥Φ ∞Φ°Ωε■ φα ±Φ∞Γεδ "═εΓα ≤∞εΓα".
─αδ│ ∩ε≥≡│ßφε ΓΓσ±≥Φ Σαφ│.
═α±≥≤∩φΦΘ Ω≡εΩ - τßσ≡σµσφφ ≤∞εΓΦ. ╥≤≥ αΓ≥ε∞α≥Φ≈φε
∩σ≡σΓ│≡ ║≥ⁿ± , ≈Φ
│±φ≤║ Γ│Σ∩εΓ│ΣφΦΘ εß'║Ω≥.
.╙∞εΓα ∩≡ΦΘ∞α║≥ⁿ± Γ ∩σ≡σδ│Ω ≤∞εΓ.
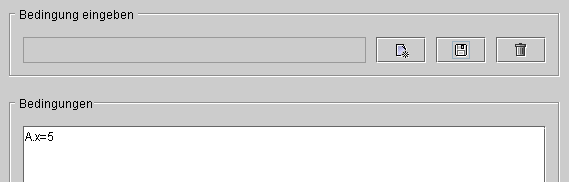
Damit sich die Bedingungen auf die Objekte in der
ZeichenflΣche auswirken, muss zum Schluss die SchaltflΣche "Schlie▀en"
bzw. "▄bernehmen" betΣtigt werden.
┘εß ≤∞εΓΦ Γ∩δΦφ≤δΦ φα εß'║Ω≥Φ ≡Φ±≤Γαδⁿφε┐ ∩δε∙ΦφΦ,
∩ε≥≡│ßφε αΩ≥ΦΓ≤Γα≥Φ Ωε∞αφΣ≤ "╟αΩ≡Φ≥Φ"
αßε "╟α±≥ε±≤Γα≥Φ".
╟∞│φα ≤∞εΓ
┘εß τ∞│φΦ≥Φ ≤∞εΓ≤, ∩ε≥≡│ßφε αΩ≥ΦΓ≤Γα≥Φ ∩σ≡σδ│Ω ≤∞εΓ. ┬
≥σΩ±≥εΓε∞≤ ∩εδ│
ΓΦß≡αφα ≤∞εΓα ∩ετφα≈α║≥ⁿ± ≈σ≡ΓεφΦ∞. ═α∩≡ΦΩ│φ÷│ τ∞│φσφα ≤∞εΓα
∩≡ΦΘ∞α║≥ⁿ± φα≥Φ±Ωε∞ ∞Φ°ΩΦ φα ±Φ∞Γεδ ΣΦ±Ωσ≥Φ.
┬ΦΣαδσφφ ≤∞εΓ
┘εß ΓΦΣαδΦ≥Φ ≤∞εΓ≤, ∩ε≥≡│ßφε ΓΦß≡α≥Φ ┐┐ Γ ∩σ≡σδ│Ω≤ ≤∞εΓ │ φα≥Φ±φ≤≥Φ φα ±Φ∞Γεδ "┬ΦΣαδΦ≥Φ"
╙∞εΓα τφΦΩα║ τ ∩σ≡σδ│Ω≤.
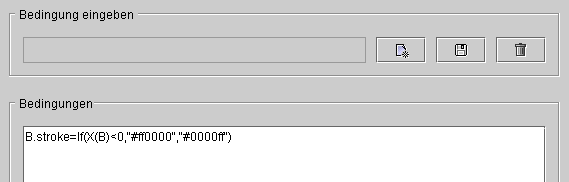
Beispiele
╧≡ΦΩδαΣΦ
- A.x=5 bewirkt, dass die x-Koordinate des freien Punktes A immer den Wert 5 besitzt.
- B.stroke=If(X(B)>0,"#ff0000","#0000ff") stellt den Punkt B rot dar, falls seine x-Koordinate kleiner 0 ist. Andernfalls wird der Punkt blau dargestellt.
- T1.visible=If(Y(C)>1,True,False) blendet den Text T1 ein, sobald die y-Koordinate von Punkt C gr÷▀er als 1 ist. Ist das nicht der Fall, verschwindet der Text.
- A.x=5 Γ∩δΦΓα║ φα ≥σ, ∙ε Ωεε≡ΣΦφα≥α X Γ│δⁿφε┐ ≥ε≈ΩΦ A ταΓµΣΦ ∞α║ τφα≈σφφ 5.
- B.stroke=If(X(B)>0,"#ff0000","#0000ff") ∩ετφα≈α║ ≥ε≈Ω≤ B ≈σ≡ΓεφΦ∞, Ω∙ε ┐┐ Ωεε≡ΣΦφα≥α X ∞σφ°α 0 . ┬ │φ°ε∞≤ ΓΦ∩αΣΩ≤ ≥ε≈Ωα ∩ετφα≈α║≥ⁿ± ßδαΩΦ≥φΦ∞.
- T1.visible=If(Y(C)>1,True,False) ΓΩδ■≈α║ ≥σΩ±≥ T1 , Ω∙ε Ωεε≡ΣΦφα≥α Y ≥ε≈ΩΦ C ß│δⁿ°α 1. ▀Ω∙ε ÷σ φσ ≥αΩ, ≥σΩ±≥ τφΦΩα║.
╬πδ Σ ∞εµδΦΓΦ⌡ Ωδ■≈εΓΦ⌡ ±δ│Γ
| ╬ß'║Ω≥ |
╩δ■≈εΓσ ±δεΓε |
╥Φ∩ |
╟φα≈σφφ |
┬σδΦ≈Φφα |
╟απαδⁿφ│ Σαφ│ Σδ Γ±Φ⌡ εß'║Ω≥│Γ |
area | int | ╤σφτΦ≥ΦΓφα ±⌠σ≡α |
╓│δ│ ≈Φ±δα |
| dash | int | ╥Φ∩ δ│φ│Θ |
0, 1, 2, ..., 7 | |
| draft | boolean | ╬ß'║Ω≥Φ Γ ≡σµΦ∞│ ∩≡εσΩ≥α |
False / True | |
| draftcolor | Color | ╩εδ│≡ ≡σµΦ∞≤ ∩≡εσΩ≥α |
├σΩ±αΣσ÷Φ∞αδⁿφΦΘ ∩εΩατφΦΩ ⌠α≡ß |
|
| fill | Color | ╩εδ│≡ τα∩εΓφσφφ |
├σΩ±αΣσ÷Φ∞αδⁿφΦΘ ∩εΩατφΦΩ ⌠α≡ß |
|
| info | String | ▓φ⌠ε≡∞α≥ΦΓφΦΘ εß'║Ω≥ | ╥σΩ±≥ |
|
| label | Color | ╩εδ│≡ ∩│Σ∩Φ±│Γ |
├σΩ±αΣσ÷Φ∞αδⁿφΦΘ ∩εΩατφΦΩ ⌠α≡ß |
|
| lighting | Color | ╩εδ│≡ ∞α≡Ω≤Γαφφ |
├σΩ±αΣσ÷Φ∞αδⁿφΦΘ ∩εΩατφΦΩ ⌠α≡ß |
|
| showinfo | boolean | ╧εΩατ │φ⌠ε≡∞α÷│┐ ∙εΣε εß'║Ω≥α | False / True | |
| stroke | Color | ╩εδ│≡ Ωεφ≥≤≡≤ |
├σΩ±αΣσ÷Φ∞αδⁿφΦΘ ∩εΩατφΦΩ ⌠α≡ß |
|
| strokewidth | double | ╥εΓ∙Φφα δ│φ│Θ |
─σ± ≥ΩεΓΦΘ Σ≡│ß |
|
| trace | boolean | ╨σµΦ∞ ±δ│Σ≤ |
False / True |
|
| visible | boolean | ┬ΦΣΦ∞│±≥ⁿ |
False / True |
|
| ╧≡ ∞α |
editable | boolean | ╠εµδΦΓ│±≥ⁿ ∩σ≡σ⌡εΣ≤ ∞│µ Γ│Σ≡│τΩε∞,
φα∩│Γ∩≡ ∞ε■, ∩≡ ∞ε■ |
False / True |
| first | boolean | ╧≡εΣεΓµΦ≥Φ τα ∩ε≈α≥ΩεΓ≤ ≥ε≈Ω≤ |
False / True |
|
| last | boolean | ╧≡εΣεΓµΦ≥Φ τα Ω│φ÷σΓ≤ ≥ε≈Ω≤ |
False / True |
|
| ╩εΓτφα ≥ε≈Ωα |
animated | boolean | └φ│∞α÷│ ΩεΓτφε┐ ≥ε≈ΩΦ |
False / True |
| direction | boolean | ═α∩≡ ∞ ≡≤⌡≤ ΩεΓτφε┐ ≥ε≈ΩΦ |
False / True |
|
| free | boolean | ╟Γ│δⁿφσφφ ΩεΓτφε┐ ≥ε≈ΩΦ Γ│Σ ±Γεπε εß'║Ω≥≤-φε±│ |
False / True |
|
| position | double | ╧ετΦ÷│ ΩεΓτφε┐ ≥ε≈ΩΦ φα εß'║Ω≥│ | ─σ± ≥ΩεΓΦΘ Σ≡│ß |
|
| ─≤πα Ωεδα |
firstarrow | boolean | ╨≤⌡ ±≥≡│δΩΦ ∩≡ε≥Φ πεΣΦφφΦΩεΓε┐ ±≥≡│δΩΦ |
False / True |
| fullcircle | boolean | ╩εδε Ω ∩≡ΦΩδαΣ ∩εΓεΣµσφφ ΩεΓτφΦ⌡ ≥ε≈εΩ |
False / True |
|
| lastarrow | boolean | ╨≤⌡ ±≥≡│δΩΦ τα πεΣΦφφΦΩεΓε■ ±≥≡│δΩε■ |
False / True |
|
| ╥ε≈Ωα |
constructionline | boolean | ┬ΦΣ│δσφφ δ│φ│Θ ∩σ≡σ≥Φφ≤ ∩≡Φ ≥ε≈Ωα⌡ ∩σ≡σ≥Φφ≤ |
False / True |
| coordinates | boolean | ╧ετφα≈σφφ Ωεε≡ΣΦφα≥ ≥ε≈ΩΦ |
False / True |
|
| fix | boolean | ╧≡ΦΩ≡│∩δσφφ ≥ε≈ΩΦ |
False / True |
|
| style | int | ┬Φπδ Σ ≥ε≈ΩΦ |
0, 1, 2, ..., 13 | |
| x | double | └ß±÷Φ±α ≥ε≈ΩΦ |
─σ± ≥ΩεΓΦΘ Σ≡│ß |
|
| y | double | ╬≡ΣΦφα≥α ≥ε≈ΩΦ |
─σ± ≥ΩεΓΦΘ Σ≡│ß |
|
| ╥σΩ±≥ |
autodigits | boolean | └Γ≥ε∞α≥Φ≈φσ ΓΦτφα≈σφφ Ω│δⁿΩε±≥│ ≡ετ≡ Σ│Γ ∩│±δ Ωε∞Φ ∩≡Φ εß≈Φ±δσφφ ⌡ |
False / True |
| digits | int | ╩│δⁿΩ│±≥ⁿ ≡ετ≡ Σ│Γ ∩│±δ Ωε∞Φ ∩≡Φ εß≈Φ±δσφφ ⌡ |
0, 1, ..., 5 | |
| fix | boolean | ╧≡ΦΩ≡│∩δσφφ ≥σΩ±≥≤ |
False / True |
|
| x | double | └ß±÷Φ±α ≥σΩ±≥≤ |
─σ± ≥ΩεΓΦΘ Σ≡│ß |
|
| y | double | ╬≡ΣΦφα≥α ≥σΩ±≥≤ |
─σ± ≥ΩεΓΦΘ Σ≡│ß |
|
| ─≤πα ÷σφ≥≡αδⁿφεπε Ω≤≥α |
radius | double | ╨αΣ│≤± Σ≤πΦ ÷σφ≥≡αδⁿφεπε Ω≤≥α |
─σ± ≥ΩεΓΦΘ Σ≡│ß |
| text | String | ╟α∩Φ± Ω≤≥α |
╥σΩ±≥ |
─ΦΓ.≥αΩεµ:
┬δα±≥ΦΓε±≥│ εß'║Ω≥α
╤│≥Ωα
╤Φ±≥σ∞α
Ωεε≡ΣΦφα≥
╧≡αΓΦδα εß≈Φ±δσφⁿ